BlockChain : les adresses sont-elles sécurisées ?
Tout utilisateur de BlockChain est représenté par un trio de grands nombres : l’adresse qu’il utilise sur la BlockChain, la clé publique qui permet à chacun de vérifier les transactions de cet utilisateur et la clé privée que l’utilisateur garde secrètement et qui lui permet de signer ses transactions. Usurper l’identité d’un utilisateur sur une BlockChain revient donc à s’accaparer ce trio. On est donc en droit de se demander à quel point le système est sécurisé.
Retour technique sur la génération de ce trio : Prenez une chaîne de caractères, appelez-la clé privée, utilisez un algorithme mathématique pour calculer ce qu’on appelle la clé publique, compressez cette clé avec un autre algorithme et vous obtenez une adresse, dernier des éléments pour pouvoir agir sur une BlockChain. Cela semble si facile qu’on peut se demander si le système est réellement sécurisé. Au risque de vous dévoiler immédiatement la conclusion, il n’est pas impossible d’utiliser l’adresse BlockChain d’un autre.
Injection, Surjection, Bijection
Les notions de mathématiques utilisées dans cet article seront limitées, mais il en faut néanmoins quelques-unes pour comprendre certains concepts. La première notion représente l’utilisation d’un ensemble au travers d’une fonction.
Dans l’introduction, il est écrit : “appelez-la clé privée, utilisez un algorithme pour calculer ce qu’on appelle la clé publique”. Cela signifie qu’on passe de l’ensemble des clés privées à l’ensemble des clés publiques à l’aide d’un algorithme. Mais on est en droit de se demander si on y gagne (injection), si on y perd (surjection) ou si rien ne change (bijection).
https://blog.worldline.tech//images/post/01-injection.png does not exist {: .center} Figure 1 - Injection
On parle d’injection quand l’ensemble d’arrivée est plus grand que l’ensemble de départ. Il y a donc des éléments de l’ensemble d’arrivée qui ne peuvent pas être atteints.
https://blog.worldline.tech//images/post/02-surjection.png does not exist {: .center} Figure 2 - Surjection
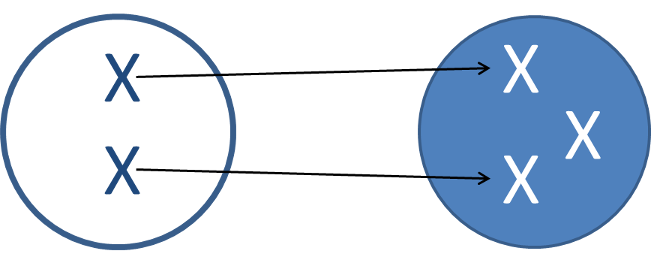
On parle de surjection quand l’ensemble d’arrivée est plus petit que l’ensemble de départ. Il y a plusieurs éléments de l’ensemble de départ qui peuvent mener à un même élément de l’ensemble d’arrivée.
https://blog.worldline.tech//images/post/03-bijection.png does not exist {: .center} Figure 3 - Bijection
On parle de bijection lorsque les deux ensembles ont la même taille et que tout élément de l’ensemble de départ correspond à un et un seul élément de l’ensemble d’arrivée.
Du point de vue de la sécurité, on préfère ne pas réduire les ensembles par l’utilisation de méthodes, on préfère donc naturellement l’injection ou la bijection. Si on ajoute un souhait d’efficacité, et ne pas avoir d’éléments qui ne servent à rien, alors la bijection est de mise.
Qu’en est-il de nos clés et adresses ?
En ce qui concerne les clés, privées et publiques, elles sont calculées par l’utilisation de courbes elliptiques appelées secp256k1, c’est-à-dire que les clés ont une longueur de 256 bits, donc on peut générer 2^256 clés publiques à partir de 2^256 clés privées, il y a une bijection entre les deux ensembles.
L’adresse, par contre, est une “compression” base58 de la clé publique, basée sur un algorithme appelé RIPE-MD160, c’est-à-dire que les adresses ont une longueur de 160 bits, on peut donc en générer 2^160.
Le passage de la clé publique à l’adresse est donc surjectif.
Deux clés publiques peuvent mener à la même adresse.
Finalement, il ne faut pas parler de 2^256 clés, mais de 2^160 possibilités d’ouvrir un coffre BlockChain.
Dit autrement, puisque deux jeux de clés permettent d’utiliser une même adresse, une faille de sécurité a d’avantages de risques d’arriver par les adresses.
Nous allons donc nous intéresser à la fiabilité des adresses.
Le pouvoir des grands nombres
Le principe de l’adressage dans la BlockChain revient à dire : “voici un champ, prenez un caillou et cachez votre coffre sous votre caillou à la vue de tout le monde”. Dès lors, il est compliqué d’y voir un système sécurisé puisque nous pensons avec des nombres “standards”, c’est-à-dire dont notre cerveau peut concevoir l’ordre de grandeur.
Cachons un billet sous un caillou au milieu de pelouse. Si une personne sait qu’il y a un billet sous un caillou, combien de temps faudra-t-il pour que le billet soit découvert ?
Multiplions par dix le nombre de cailloux. Evidemment, la recherche est plus compliquée, mais on ne peut toujours pas parler de système sécurisé.
Multiplions encore par dix. Cent cailloux ! Toujours pas.
Multiplions encore par dix pour arriver donc à mille cailloux. Est-ce suffisamment sécurisé ? Combien de temps pouvons-nous laisser les cailloux sans surveillance directe ?
Multiplions par cent, soit cent mille cailloux. Cette fois-ci, combien de temps peut-on s’éloigner sereinement des cailloux sans crainte que le billet ne soit découvert ?
Si la personne retourne un caillou à chaque seconde, sans s’arrêter en conservant toujours le même rythme, elle aura besoin d’un peu plus de 27h pour retourner tous les cailloux. Et même si elle réduit le temps en utilisant les deux mains, cela laisse approximativement 13h.
100.000 s’écrit avec 5 zéros, une façon de l’écrire est donc 1 x 10^5.
Il existe 2^160 adresses possibles, cela correspond à 1,46 x 10^48, un chiffre qui compte pas moins de 48 zéros. Le nombre est tellement grand qu’il est impossible d’imaginer ce qu’il représente. Alors essayons de le comparer à la puissance de calcul des ordinateurs et à des statistiques connues.
Sécurisation de coffre
Ce qui importe avant tout, c’est que notre adresse soit sécurisée, c’est-à-dire que personne d’autre que nous-même peut utiliser notre propre adresse. Si elle devait faire face à 1000 ordinateurs qui peuvent essayer 100 combinaisons par seconde, il faudrait à ces ordinateurs 1,46 x 10^43 secondes pour faire le tour des adresses, c’est-à-dire 4,6 x 10^35 années. Pour rappel, 100.000 ans s’écrivent 1 x 10^5 années.
La chance de gagner le premier rang de l’EuroMillion est de 1/140.000.000.
Avec des ordinateurs pouvant essayer 1000 combinaisons par seconde, donc dix fois plus que précédemment, et travaillant pendant une année complète, il faudrait 330.985.967.327.408.034.741.300.125.174 (i.e. 3 x 10^29 ) ordinateurs pour arriver à la même chance que de gagner à l’EuroMillion.
Comment augmentent les chances avec l’arrivée de nouveaux utilisateurs ? Dit autrement, puisque notre adresse est sécurisée, transformons-nous en chercheur de trésor et essayons d’ouvrir une adresse quelle qu’elle soit. Sur Bitcoin, qui est peut-être le plus grand réseau BlockChain, on compte un peu moins d’un million d’adresses actives. Sur 1,46 x 10^48 adresses initialement possibles, le changement est imperceptible, les adresses actives sont des aiguilles dans des bottes de foin. C’est à nouveau, la puissance des grands nombres. Il est évident qu’une voiture avance beaucoup du point de vue d’un piéton. Mais elle avance moins du point de vue d’une montgolfière qui voit la voiture comme une fourmi. Et cette voiture devient immobile vue de la lune. Qu’en est-il vu de Pluton ? La variation sur le nombre d’adresses Bitcoin est, en fait, immensément inférieure à la variation de 1mm d’une voiture vue depuis Pluton.
Loi de Moore
La loi de Moore parle d’une multiplication par deux de la puissance de calcul tous les 18 mois. On sait que cette loi est très optimiste, mais conservons-la comme repère. Combien de temps le système va-t-il conserver ce niveau de sécurité ?
Si les derniers ordinateurs décrits précédemment peuvent réaliser 1000 combinaisons par seconde, alors dans 30 ans, ils seront, au mieux, capables d’exécuter 524.288.000 transactions par seconde. Si nous utilisons 1000 ordinateurs d’une telle puissance alors il faudra encore 8,8 x 10^29 années pour essayer les 2^160 combinaisons. Pour rappel, 100.000 ans s’écrivent 1 x 10^5 années.
Conclusion
L’objectif de l’article était de vous donner tous les éléments nécessaires pour vous permettre de décider par vous-même si les adresses BlockChain sont sécurisées ou non. Comme annoncé dès l’introduction, il n’est pas impossible de réussir à trouver une clé qui permette d’utiliser l’adresse BlockChain d’un autre. En revanche, cet article a tenté d’expliquer que, par l’utilisation des grands nombres, le temps nécessaire pour y parvenir est inimaginable. Inimaginable signifie qu’avec 1000 ordinateurs qui testent 100 combinaison par seconde, il faudrait 460.000.000.000.000.000.000.000.000.000.000.000 années.